There’s an old motivational story that goes like this: a teacher stands in front of his classroom and places on his desk an empty jar. He then takes out a bag of large rocks and carefully fills the jar to the brim. He asks his students if the jar is full, and most agree that it is. The teacher then takes out a bag of gravel, and shakes its content into the jar, filling in the spaces that were left between the larger rocks. Once more, he asks his students if the jar is full, only this time the students seem unsure. He then proceeds to take a smaller jar filled with sand, and pour it on top of the gravel and rocks, filling every crevice and crack. Now the students know he isn’t done, and finally, he sprinkles water on top of everything else.
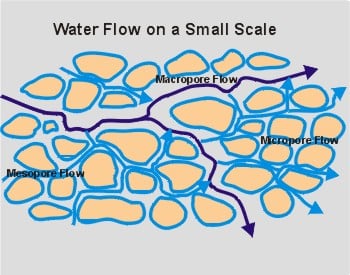
While this is a great motivational story, it also teaches us that the particle size of the biomass has an effect on extraction efficiency. Just like the rocks and gravel and sand all went into the jar, cannabis plant matter is packed into an extraction column. In a closed-loop extraction, the solvent is pumped in from the top, allowed to soak the biomass for a few minutes, then moved to a collection vessel from the bottom. When the particles are large, even when the material is packed as tightly as it can, air pockets tend to form in the inner recesses of the extraction column. [1] When solvent is pumped in, those pockets create channels for the liquid to run down, making it so that the solvent is less likely to soak into the plant material, reducing the efficiency of the extraction.
While today a plethora of data has been published aimed at determining how best to extract cannabinoids from cannabis biomass, a decade ago, very little literature existed regarding the optimal conditions for different types of cannabis extraction. This is because of the underground nature of the industry at the time.
Even so, some work had been done to determine the parameters of working with cannabis. This work was mainly done by forensic scientists who were analyzing seized cannabis for taxonomic analysis, as they tried to determine the origin of the plants and their relative strength. [2] Among other things, these scientists wrote about the effects that particle size has on the extraction efficiency of cannabis. [3] They took small, equal masses of cannabis and subjected them to different types and strengths of grinds—just like with coffee!
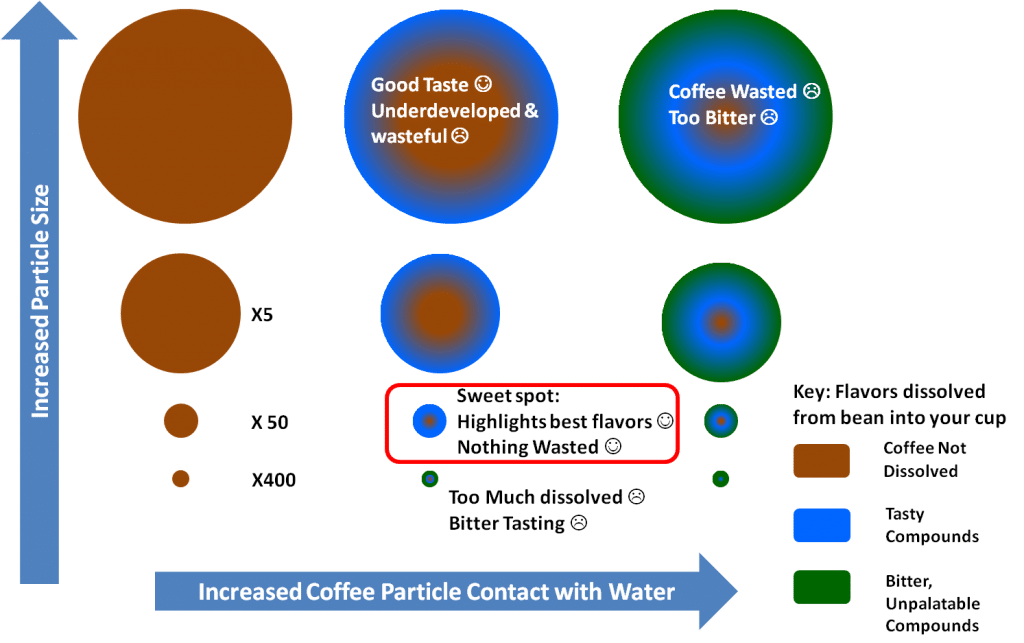
The published results showed that the finer the grind of the cannabis, the more cannabinoids were successfully extracted. [4] This should intuitively make sense. Particle size affects extraction efficiency because the amount of active compounds that are extracted are directly proportional to the surface area of the particles inside the extraction vessel. Surface area is a function of the particle size, with a collection of larger particles having, overall, less surface area for extraction than a collection of an equal mass of smaller particles.
While it is theoretically possible to stuff together any kind of material, uniform or uneven, small or large particulates, there are certain issues that must be considered when preparing the biomass starting material. Running a method validation when beginning to extract with a new instrument will help determine the optimal particle size for your extraction technique.
References
- “Cannabis Extraction by Supercritical Carbon Dioxide – Selection and Preparation of Feed Stock”. Supercritical Fluid Technologies, Inc. Accessed May 11, 2019.
- Dufresnes, C. et al. “Broad-Scale Genetic Diversity of Cannabis for Forensic Applications”. PLoS One. 2017; 12(1): e0170522 [Times cited = 11, Journal impact factor = 2.766].
- Eory, L. et al. “Supercritical Fluid Extraction Of Tetrahydrocannabinol From Marihuana Study Of The Effect Of Particle Size”. Problems of Forensic Sciences. 2001; 162: 322-7 [Times cited = 3, Journal impact factor = 0.118].
- Xiangyu, Y. et al. “Extraction and Analysis of Tetrahydrocannabinol, A Cannabis Compound in Oral Fluid”. International Journal of Biology. 2017; 9(1): 30-35 [Times cited = 1, Journal impact factor = 3.873].